FG09 UVB
The ionizing background, from the ultraviolet to the x-rays, is a fundamental ingredient to both theoretical and empirical studies of both the intergalactic medium and galaxy formation as it determines the ionization balance of light elements as well as the thermal history of cosmic gas through photoheating.
Its spectrum is therefore a key input to both hydrodynamical cosmological simulations and studies of metal abundances, which require ionizing corrections to relate the observed ions to total elemental abundances.
As part of my Ph.D thesis, I combined intergalactic opacity measurements and recent luminosity function measurements to constrain the magnitude, evolution, spectral shape, and sources of the ionizing background, ultimately resulting into a new and improved calculation of its spectrum. This page provides links to this work as well as electronic data tables for researchers to use in their own work.
Following are also remarks on the applicability and limitations of this spectrum, as well as important related information and pointers to other tools and references.
Electronic Data
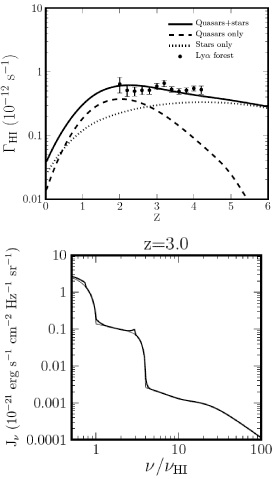
Following are links to data from our ionizing background spectrum paper (arXiv:0901.4554 [1]) in electronic form. The ionizing background in our fiducial model has contributions from both quasars and star-forming galaxies, with the latter dominating at approximately z>3. In addition to being compatible with recent luminosity functions, the model was calibrated to satisfy the measured mean transmission of the Ly-alpha forest at intermediate redshifts (z=2-4.2, [4]), published HeII to HI column density ratios, HeII reionization by z~3, and complete HI reionization by z=6 [2, 3].
Includes a table of photoionization and photoheating rates, and full UV background spectra versus redshift. To use the model in your GADGET simulations, simply rename the file ‘TREECOOL_fg_dec11’ -> ‘TREECOOL’ and replace the copy in your GADGET directory. For more details, see the included README.
The December 2011 update includes larger redshift and frequency ranges, better convergence properties at high redshift, and corrects a normalization inconsistency between the individual spectra and the integrated rates.
Applicability and Limitations
The spectra downloadable above were obtained by solving the cosmological radiative transfer equation for the average specific intensity, J_nu(z). This specific intensity should be valid in most of the volume of the Universe (in particular, for the systems that constitute most of the Ly-alpha forest), with important exceptions and qualifications.
A full characterization of the ionizing background spectrum, including its variations within self-shielded systems and in proximity of bright sources, and its random fluctuations is still an open problem. It is therefore important that studies that use average calculations like ours be aware of its limitations and apply appropriate care depending on the regime they are studying.
Self-Shielded Systems and Local Sources
At a given energy, the spectrum will be significantly attenuated within systems that self-shield themselves from external radiation. The interiors of HI Lyman limit systems with N_HI>10^17.2 cm^-2 (corresponding to an optical depth of unity at 1 Ryd), for example, will see an attenuated spectrum above 1 Ryd.
Systems that are located in close proximity of luminous quasars and galaxies will also see a different spectrum, dominated by the local sources rather than the cosmological flux. Note that these systems, associated with overdense regions, may correlate with those that self-shield (e.g., Miralda-Escudé 2005, ApJ, 620, 91; Schaye 2006, ApJ, 643, 59). The detailed preprint astro-ph/0307557 by Boksenberg, Sargent, & Rauch discusses some of these effects in the context of a metal absorption study.
Fluctuations
Even systems that are optically thin may see a spectrum that differs from the calculated J_nu if the local value deviates from the average owing to random fluctuations. Whether this is likely to be the case depends on the energy range and redshift of interest; the key parameter is the number of sources within one photon mean free path.
Between 1 Ryd and 4 Ryd, where galaxies contribute significant flux and the mean free path is relatively large, the fluctuations should be small at most redshifts (see the discussion in section 7 of our paper [1]). Just above 4 Ryd, the background is assumed to be dominated by much rarer quasars and the mean free path is also shorter; the fluctuations at these energies are expected to be more substantial. At higher energies, the number density of the quasar sources remains constant while the mean free path increases so we expect the fluctuations to be reduced.
For studies of fluctuations in the HI ionization background, see Meiksin & White (2003, MNRAS, 342, 1205; 2004, 350, 1107). For fluctuations in the HeII ionizing background, see Bolton et al. (2006, MNRAS, 366, 1378) and Furlanetto (arXiv:0812.3411; arXiv:0901.2584).
Hard X-rays and Type II Quasars
Because the photoelectric cross sections of hydrogen and other elements decrease with increasing energy above their ionization edges, some quasars can appear obscured in the UV yet be visible in sufficiently hard x-rays. Obscured quasars are often labelled ‘Type II’. Our calculations do not at present explicitly include Type II quasars and likely underestimate the intensity of the background above ~1 keV or so. For a recent synthesis of the cosmic x-ray background and AGNs, see Gilli et al. (2007, A&A, 463, 79). I hope to eventually provide more accurate models of the x-ray background.
Even if many quasars are obscured in the UV, the normalization of our background calculations should be valid in this regime. In fact, our calculations are based on the observed B-band quasar luminosity function (rest frame 4400 A; Hopkins et al. 2007, 654, 731). In unified AGN models, obscuration results in effective beaming of the radiation. While only a fraction of the 4*pi solid angle on average transmits UV radiation, the luminosity of each quasar is overestimated by the inverse factor by assuming isotropy. As a result, the cosmological emissivity is accurately accounted for. In the end, we also make sure that our spectra satisfy constraints on the IGM opacity, which are sensitive to the totality of the ionizing emissivity.
Reionization Events
The spectra provided are valid after reionization only. For the HI ionizing part, this means z<~6 and for the HeII ionizing part, z<~3. Within regions of the Universe that have yet to be reionized, the spectra are strongly suppressed above the corresponding ionization edge. See section 7 of our paper [1] for a discussion of the effects of reionization events on the background spectrum. Hydrodynamical Simulations
One of the main uses of our results is as a prescription for cosmological hydrodynamical simulations in the form of photoionization and photoheating rates. In most cases, the codes assume that these rates are spatially uniform, i.e., optically thin radiative transfer. This is the case in particular for GADGET-2 (Springel 2005, 354, 1105), which solves for the ionization and thermal balance following the equations laid down in Katz et al. (1996, ApJS, 105, 19).
This has two important consequences connected to reionization.
First, because the radiative transfer during reionization is very optically thick and spatially inhomogeneous, the history of reionization will not be accurately modeled by using optically thin photoionization rates. Of particular note, when we say that our model is calibrated so that HI reionization is complete by z=6 and HeII reionization by z~3, we mean that the sources of the background produce ionizing photons at a rate sufficient to reionize these elements by these redshifts, accounting for recombinations. This does not mean that using the provided photoionization rates in a code that assumes optically thin radiative transfer will yield reionization by the correct redshifts; in fact, this will likely not be the case. In our paper [2], we show how to correctly calculate the reionization history given the evolution of the ionizing sources.
Second, for a similar reason, the optically thin photoheating rates will not accurately capture the heat input during reionization events. This is particularly important for HeII reionization, which likely occurs at redshifts z~3-4 that are already commonly probed by observations and which could inject as much as ~15,000 K of heat into the IGM. We show how to analytically estimate the heat input of HeII reionization in section 7 of our paper [1]. For 3D numerical radiative transfer calculations of HeII reionization, see McQuinn et al. 2009, ApJ, 694, 842.
Finally, by calibration, our spectra should approximately reproduce the measured Ly-alpha forest mean transmission,
Useful Links
– Cloudy: A photoionization package, particularly useful for metal absorption line studies. This will tell you the ionization states of elements in a system illuminated by a given spectrum (e.g., the one we provide). Useful, for example, to measure the total mass of carbon given CIV absorption.
– HRH07 QLF: The Hopkins et al. 2007, 654, 731 quasar luminosity function in electronic form.
– GADGET: The excellent cosmological N-body/SPH simulation code written and maintained by Volker Springel.
Bibliography
1. Faucher-Giguère, C.-A., Lidz, A., Zaldarriaga, M., & Hernquist, L. 2009, “A New Calculation of the Ionizing Background Spectrum and the Effects of HeII Reionization,” ApJ, 703, 2.
2. Faucher-Giguère, C.-A., Lidz, A., Hernquist, L., & Zaldarriaga, M. 2008, “Evolution of the Intergalactic Opacity: Implications for the Ionizing Background, Cosmic Star Formation, and Quasar Activity,” ApJ, 688, 85.
3. Faucher-Giguère, C.-A., Lidz, A., Hernquist, L., & Zaldarriaga, M. 2008, “A Flat Photoionization Rate at z=2-4.2: Evidence for a Stellar-Dominated UV Background and Against a Steep Decline of Star Formation Beyond z~3,” ApJL, 682, 9.
4. Faucher-Giguère, C.-A., Prochaska, J. X., Lidz, A., Hernquist, L., & Zaldarriaga, M. 2008, “A Direct Precision Measurement of the Intergalactic Lyman-alpha Opacity at z=2-4.2,” ApJ, 681, 831.